Lattice Paths

Starting in the top left corner of a \(20 \times 20\) grid, and only being able to move to the right and down, there are exactly \(6\) routes to the bottom right corner.

How many such routes are there through a \(20 \times 20\) grid?

Let’s make it easier

When I saw this problem for the first time my first thought was that I probably can calculate it with a pen and paper.

But since we’re coding in Scala here, let’s try to make an application that will solve it for us.

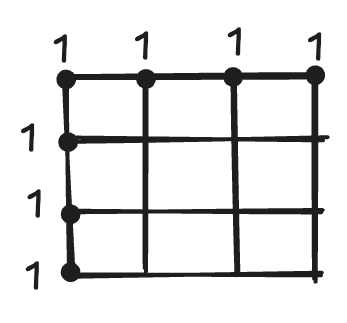
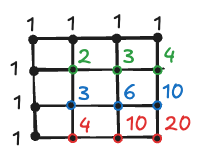
\(20 \times 20\) is a big array, too big to reason about it, while the \(2 \times 2\) is a bit too small. Let’s then draw a \(3 \times 3\) one and mark the edges with dots. How many ways to we have to reach each of these dots? Exactly one way. That was the easiest part.

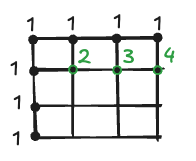
Now let’s try a second row. If we know how to get to the dot above and to the dot on the left side, then we also know how to go to the dot in question, because from their positions there’s just one way to continue (either left or down).

So, we can fill the second row starting from the left side. First dot will be \(1 + 1 = 2\), second will be \(3 + 1 = 3\), third one will be \(3 + 1 = 4\)

The third row will be no different, let’s continue the process:

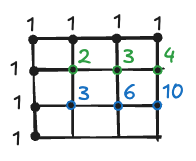
And the same goes for the last one. The answer to a question in how many possible ways we can reach the last lattice can be found in the bottom right corner: 20.

Solution

The previous section shown us some properties of the lattice paths. We can now implement the algorithm that we used. I went for a functional, recursive solution, but a mutable one that’s based on a simple 2-dimensional Array could do as well.

import scala.annotation.tailrec

object Euler015 extends EulerApp {
  override def execute(): Long = countLatticePaths(21, 21)

  private def countLatticePaths(length: Int, height: Int): Long = {
    val lattice = fillLatticeArray(length, height)
    lattice(length - 1)(height - 1)
  }

  @tailrec
  private def fillLatticeArray(length: Int, height: Int, currentResult: Seq[Seq[Long]] = Seq.empty): Seq[Seq[Long]] =
    currentResult match {
      // First row, we'll fill it with ones
      case Nil =>
        fillLatticeArray(
          length,
          height,
          Seq(Seq.fill(length)(1L))
        )
      // All rows filled, time to finish
      case other if other.size == height => currentResult
      // Filling the next row, but not the first one
      case other =>
        val nextRowNum = currentResult.size
        val previousRow = currentResult(nextRowNum - 1)
        fillLatticeArray(
          length,
          height,
          currentResult :+ previousRow.foldLeft(List.empty) { case (result, previousRowNum) =>
            result :+ result.lastOption.getOrElse(0L) + previousRowNum
          }
        )
    }
}

It does exactly what we did manually, but on a larger scale. It fills the first row and first column with ones, and then it calculates next elements from left to right, top to bottom. The answer is, as before, in the bottom right corner.

It’s a bit robust, but works pretty fast. What could you improve there?

Tip

Before continuing, think about how can we improve the solution. Can we make it more memory efficient? Can we make it faster? Do we calculate something that’s not needed for the answer?

Mutable solution

It’s not a surprise that making it mutable will make it faster. Just keep in mind that in non-algorithmic tasks the performance gainst might be miniscule, completely outweighed by all the downsides of making it mutable.

So, the first change would be to switch the Seq to an Array. What else can we do?

Previously, we stored all the intermediate results and created a complete, large array with all the values. In fact, we can calculate the next row knowing the previous row. We don’t need to remember all the other ones. Which means that there’s no need to maintain a 2-dimensional Array.

My first thought was that we need two arrays, for the current and the previous row. Can we use just one?

In the example with four lattices, the second row contained the following values: \(1, 2, 3, 4\)

If we wanted to calculate the third row by mutating the \(1, 2, 3, 4\) one, then:

• Nothing changes for the first element. It stays as one.
• We add the previous element to the next element, that is, \(1 + 2\), and the second element is \(3\). Our row is now \(1, 3, 3, 4\).
• We do the same for the third element, our row is now \(1, 3, 6, 4\)
• And the last element is calculated with \(6 + 4 = 10\), the row is now equal to \(1, 3, 6, 10\)
• For the next row, we do the same again. \(1\) stays unchanged, the second number if \(4\), another one is \(9\), and so on…

In short, now we only need to keep one row in the memory. Here’s the implementation:

object Euler015M extends EulerApp {
  override def execute(): Long = countLatticePaths(21, 21)

  private def countLatticePaths(length: Int, height: Int): Long = {
    val prevRow = Array.fill(length)(1L)

    for (_ <- 1 until height) {
      for (col <- 1 until length) {
        prevRow(col) += prevRow(col - 1)
      }
    }

    prevRow(length - 1)
  }
}

Epilogue

Going forward, we could also use this finding to improve the original, immutable solution. But maybe there’s no need to run this iterative computation at all? If you look at those numbers, they seem to be following a certain pattern.